Profunctors form a compact closed category

Compact closed categories(7)
Dual object in a SMC(1)

The dual for an object \(c \in Ob(\mathcal{C})\), which is part of a symmetric monoidal category \((\mathcal{C},I,\otimes)\).

Three consituents:

  1. An object \(c^* \in Ob(\mathcal{C})\) called the dual of c

  2. A morphism \(I\xrightarrow{\eta_c}c^* \otimes c\) called the unit for c

  3. A morphism \(c \otimes c^* \xrightarrow{\epsilon_c}I\) called the counit for c

These are required to satisfy two commutative diagram relations (snake equations)

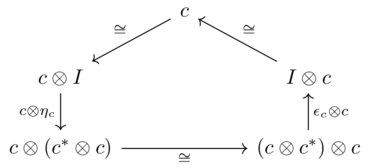
and

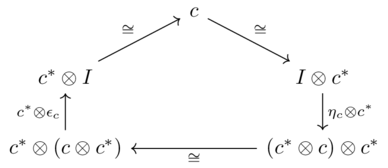
Linked by

Compact closed SMC(1)

A compact closed symmetric monoidal category

One for which every object there exists a dual. This allows us to use the following morphisms without reservation:

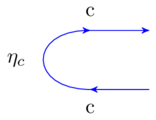
and

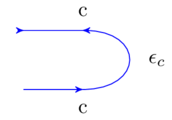
This also allows us to use the following snake equations in wiring diagrams without reservation:

and

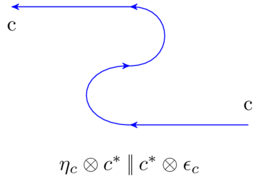
Linked by

Compact closed properties(2)

If \(\mathcal{C}\) is a compact closed category, then:

  1. \(\mathcal{C}\) is monoidal closed

  2. the dual of c is unique up to isomorphism

  3. \(c \cong (c^*)^*\)

Proof(1)

Not really proven, but: \(c \multimap d\) is given by \(c^* \otimes d\)

The natural isomorphism \(\mathcal{C}(b \otimes c, d)\cong \mathcal{C}(b,c \multimap d)\) is given by precomposing with \(id_b \otimes \eta_c\)

Correl as CCC(1)

  • The compact closed category: Corel

  • A correlation \(A \rightarrow B\) is an equivalence relation on \(A \sqcup B\)

  • Correlations are composed by the following rule: two elements are equivalent in the composite if we may travel from one to the other while staying within the component equivalence classes of either

  • There is a symmetric monoidal structure \((\varnothing, \sqcup)\). For any finite set A there is an equivalence relation on \(A \sqcup A\) that partitions elements in the first set from the second. The unit and counit are given by this partition:

    • \(\varnothing \xrightarrow{\eta_A} A \sqcup A\)

    • \(A \sqcup A \xrightarrow{\epsilon_A} \varnothing\)

Linked by

Exercise 4-62(2)

  1. Draw a picture of the unit correlation \(\varnothing \xrightarrow{\eta_{\bar 3}} \bar 3 \sqcup \bar 3\)

  2. Draw a picture of the counit correlation \(\bar 3 \sqcup \bar 3 \xrightarrow{\epsilon_{\bar 3}} \varnothing\)

  3. Check that the snake equations hold. Since every object is its own dual, only one has to be checked.

Solution(1)

  1. \(\boxed{\varnothing}\rightarrow \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\ \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\)

  2. \(\boxed{\varnothing}\leftarrow \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\ \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\)

  3. TODO

Feas as as compact closed category(5)
CCC from profunctor category(2)

Let \(\mathcal{V}\) be a skeltal quantale. The category \(\mathbf{Prof}_\mathcal{V}\) can be given the structure of a compact closed category, with the monoidal product given by the product of \(\mathcal{V}\) categories.

Proof(1)

  • Monoidal product acts on objects:

    • \(\mathcal{X} \times \mathcal{Y}((x,y),(x',y'))\) := \(\mathcal{X}(x,x') \otimes \mathcal{Y}(y,y')\)

  • Monoidal product acts on morphisms:

    • \(\phi \times \psi((x_1,y_1),(x_2,y_2))\) := \(\phi(x_1,x_2)\otimes\psi(y_1,y_2)\)

  • Monoidal unit is the \(\mathcal{V}\) category \(1\)

  • Duals in \(\mathbf{Prof}_\mathcal{V}\) are just opposite categories

    • For every \(\mathcal{V}\) category, \(\mathcal{X}\), its dual is \(\mathcal{X}^{op}\)

    • The unit and counit look like identities

      • The unit is a \(\mathcal{V}\) profunctor \(1 \overset{\eta_\mathcal{X}}\nrightarrow \mathcal{X}^{op} \times \mathcal{X}\)

      • Alternatively \(1 \times \mathcal{X}^{op} \times \mathcal{X}\xrightarrow{\eta_\mathcal{X}}\mathcal{V}\)

      • Defined by \(\eta_\mathcal{X}(1,x,x'):=\mathcal{X}(x,x')\)

      • Likewise for the co-unit: \(\epsilon_\mathcal{X}(x,x',1):=\mathcal{X}(x,x')\)

Exercise 4-64(1)

TODO

Solution(1)

TODO

Exercise 4-65(1)

TODO

Solution(0)

TODO

Exercise 4-66(1)

Check that the proposed unit and counits do obey the snake equations.

Solution(0)

TODO